ILLUSTRATION ENGINE SPEED COMPARISONS
Last year, I had a industry speaking opportunities on the topic of building life insurance actuarial calculation engines in code when traditional tools like Excel or vendor platforms may not be the right fit. I demonstrated a rudimentary approach for a basic universal life illustration engine using Python and that code used was heavily influenced by Part 6 of our calculation engine series. I also translated into two other languages for some simple speed benchmarking / comparisons and I have been meaning to share those results more broadly. Today, I’m finally getting to it. There are rudimentary implementations in Python, Go, and Rust in this repository which are based off a simple Excel model that you can download here.
BACKGROUND
I, like a lot of actuaries, have spent far too much time in Excel. It’s a workhorse for a lot of reasons and while I love it’s flexibility and accessibility in a corporate setting, it is not always the best tool for the job. I like efficient processes and early in my career that lead to learning VBA to automate things in Excel because from my perspective, more efficient processes mean I can spend less time waiting for results and more time doing work that actually adds value. This naturally has lead me down a path to exploring languages like Python, R, C, Go, Rust, etc. so I can automate tasks away or build something entirely new when Excel and vendor solutions are not the right fit. These custom solutions are not always a good fit, but I have observed increased interest in this path and wanted to share something measurable so others have more information to make decisions. Speed is fairly easy to measure.
I wanted to simulate some real use case, or part of one, so that the results feel meaningful. We could easily look up benchmarks around the internet but those are often running tests that may be hard to translate to actuarial workloads (I’m looking at you Fibonacci tests). So I decided to use a universal life illustration engine and premium solve since those feel meaty enough to provide actionable information but would not be so intense that the development would be huge. Also, I can leverage the code from the calculation engine series. So without going down an optimization rabbit hole, I started with a simple Excel model and I converted the logic to Python, Go, and Rust to see how the process performs across tools/languages. The code is not intended to represent an optimal implementation for any specific language or broader architecture design.
I picked these languages because I like Python and Go and wanted an excuse to learn a little more Rust. This will also give me an opportunity to compare an interpreted language solution (Python) against a couple of compiled language solutions (Go and Rust) since I’ll be using the standard tool chains for these.
IMPLEMENTATIONS
Three basic implementations were written in code; one in Python, one in Rust, and one in Go. I did not attempt to thoroughly optimize for each language and instead attempted to keep the implementations consistent and roughly how I thought an initial proof of concept might look. Not a ton of abstractions. Not a ton of object-oriented code. A handful of functions and some data structures/containers so the process is clear and transparent. I do not think the architecture presented is the best for a truly scalable and long-term solution.
The general idea is:
Define the characteristics of the case to run
Gather applicable rates based on the characteristics
Run illustration with specified premium or solve for level premium to reach maturity
Wrap the functionality in some simple parallel processing logic leveraging a queue or something queue-like
Each implementation is separated into 3 files:
functions: contains all the logic for running a single case; from reading rate files, to generating an illustration, to running a premium solve
parallel: contains the logic and architecture for setting up parallel processing
main: primary driver for running the benchmarking, leverages both functions and parallel
Before we get to the results I do want to highlight two things. First, when parallelizing a problem it’s not guaranteed that throwing N workers at the problem instead of 1 will yield a speed increase of N. You might get less mileage out of parallelization because of the overhead of setting up and tearing down additional workers, inter-process communication, or the problem not being CPU-bound. We should be able to measure where our process is CPU-bound (if it even is) but for this demonstration we’ll skip that. Some of the other issues are partially controllable, but not entirely, which brings me to the second thing I want to highlight. In parallel.go of the Go implementation, lines 71 and 72 create two channels for inter-process communication.
...
taskChannel := make(chan Task)
resultChannel := make(chan *Illustration, numJobs)
...
The first, taskChannel, is an unbuffered channel for Task objects that sends tasks to workers. The second, resultChannel, is a buffered channel sized relative to the number of tasks. If we make taskChannel buffered like we do resultChannel I noticed a significant degradation in speed.
RESULTS
Benchmarking code across languages is tricky and there are easy traps to fall into. It would be easy to write efficient code in one language and inefficient code in another which would yield highly distorted results. As noted earlier, the code structure was generally held consistent across languages but the comparisons are almost certainly going to be imperfect.
Additionally, Excel results presented in the following subsections are after turning off multi-threaded calculations — this provided a substantial boost (~10x for illustrations and 25x for premium solves) on my machine. If you’re struggling with run time in an Excel tool I recommend checking to see if multi-threaded calculations are actually slowing things down for you.
ILLUSTRATION
| Implementation | Run time | Excel / Implementation |
|---|---|---|
| Excel | 24.816 | 1.0x |
| Python - single | 4.818 | 5.2x |
| Go - single | 3.326 | 7.5x |
| Rust - single | 3.655 | 6.8x |
| Python - parallel | 2.142 | 11.6x |
| Go - parallel | 0.915 | 27.1x |
| Rust - parallel | 0.841 | 29.5x |
When running 1,000 illustrations there is a decent reduction in runtime compared to our Excel starting point, but there was very little difference between our Python, Rust, and Go implementations with a single worker. I suspect that the reason there is not much difference is two-fold:
The majority of run time is spent retrieving data from files (I/O bottleneck)
The rate files are small so the Python implementation performs well compared to Go and Rust which are compiled
For the parallel implementations (8 workers) Python had an additional ~2x improvement, Go had ~3.5x, and Rust had ~4.5x — none of which are close to the theoretical 8x we might expect. This might be because
The overhead incurred spinning up additional workers
Inefficient parallelization design
I also looked at running the Python, Go, and Rust implementations with 10, 100, and 10,000 cases and did not find much unexpected. The only notable thing is the parallel Python implementation seemed to suffer at low case count presumably from additional worker overhead.
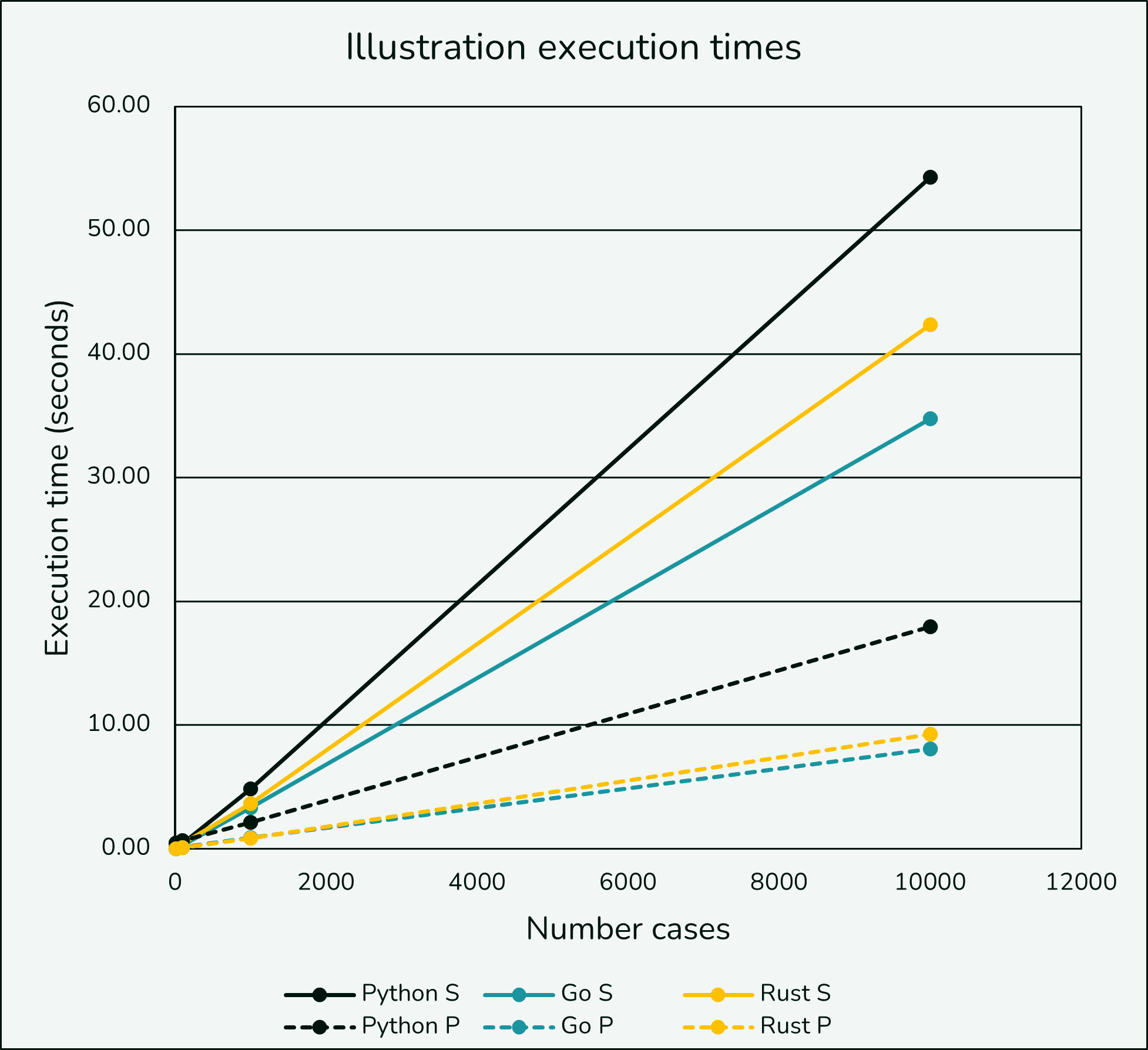
| Implementation | 10 Cases | 100 Cases | 1,000 Cases | 10,000 Cases |
|---|---|---|---|---|
| Python - single | 0.05 | 0.41 | 4.82 | 54.26 |
| Go - single | 0.05 | 0.29 | 3.33 | 34.75 |
| Rust - single | 0.04 | 0.40 | 3.65 | 42.34 |
| Python - parallel | 0.48 | 0.68 | 2.14 | 17.97 |
| Go - parallel | 0.01 | 0.11 | 0.92 | 8.09 |
| Rust - parallel | 0.01 | 0.10 | 0.84 | 9.24 |
The execution time larger looks linear as cases are added, a good sign.
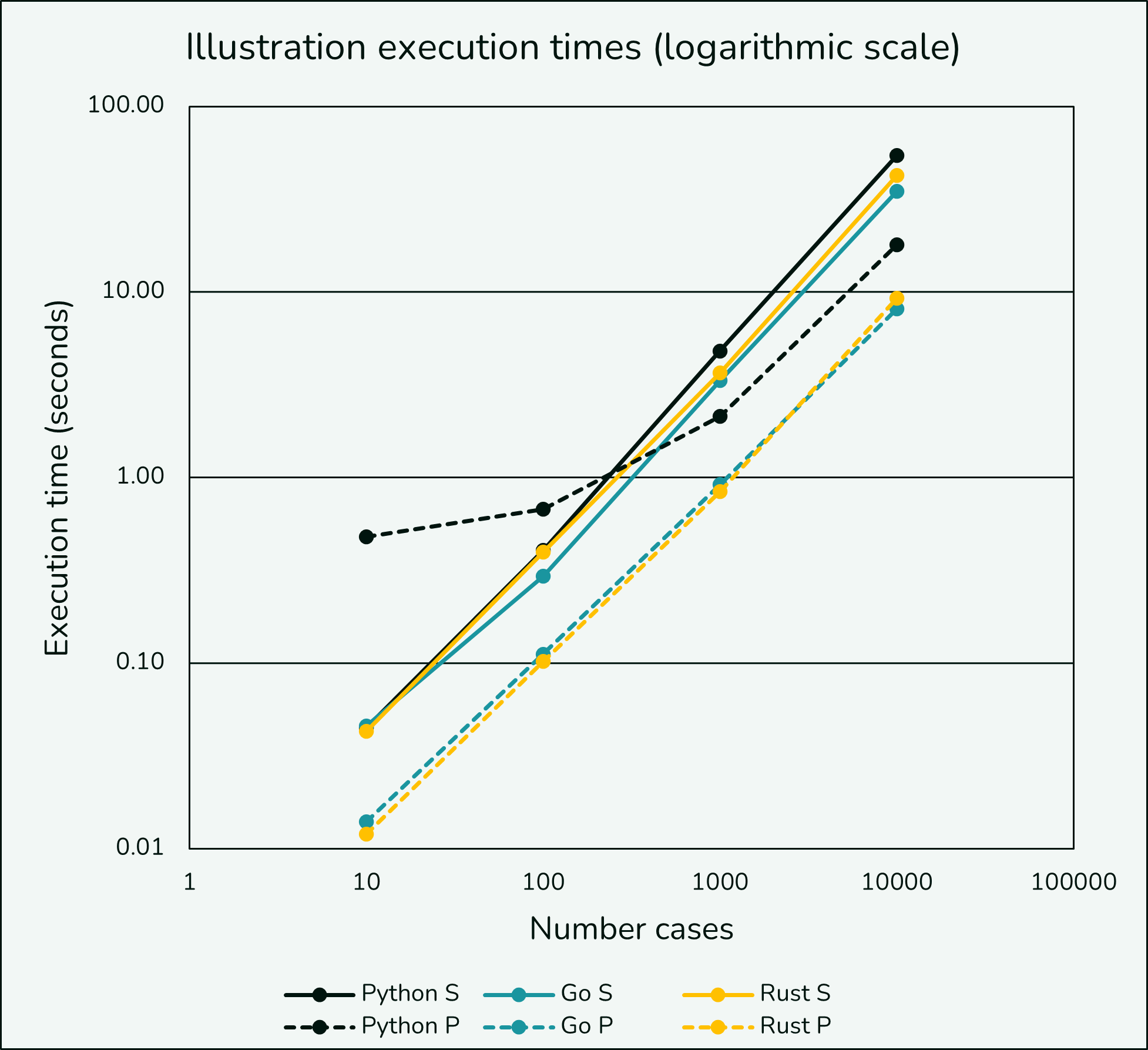
Looking instead at the data on a logarithmic scale we still generally see the linear growth, but at lower case counts we also can see the parallel Python implementation being hindered until somewhere between 100 and 1,000 cases.
PREMIUM SOLVE
| Implementation | Run time | Excel / Implementation |
|---|---|---|
| Excel* | 185.508 | 1.0x |
| Python - single | 29.409 | 6.3x |
| Go - single | 5.230 | 35.5x |
| Rust - single | 4.213 | 44.0x |
| Python - parallel | 7.942 | 23.4x |
| Go - parallel | 1.513 | 122.6x |
| Rust - parallel | 0.906 | 204.7x |
When running premium solves I noticed a few things:
The compiled implementations (Rust and Go) performed noticeably better than the interpreted implementation (Python) even when using a single worker,
Python’s parallelization performed ~3.5x better vs the ~2x on the illustrations, and
Rust really started to pull away from Go for certain case counts
While the Python implementation performs well compared to Excel (>20x when parallelized), we can see the benefits of a compiled solution on longer, more computation intensive work. Looking at 10, 100, and 10,000 cases again we find nothing unusual. Perhaps the biggest find was that as case counts increased the difference between Go and Rust started to shrink, most notably at 10,000 cases.
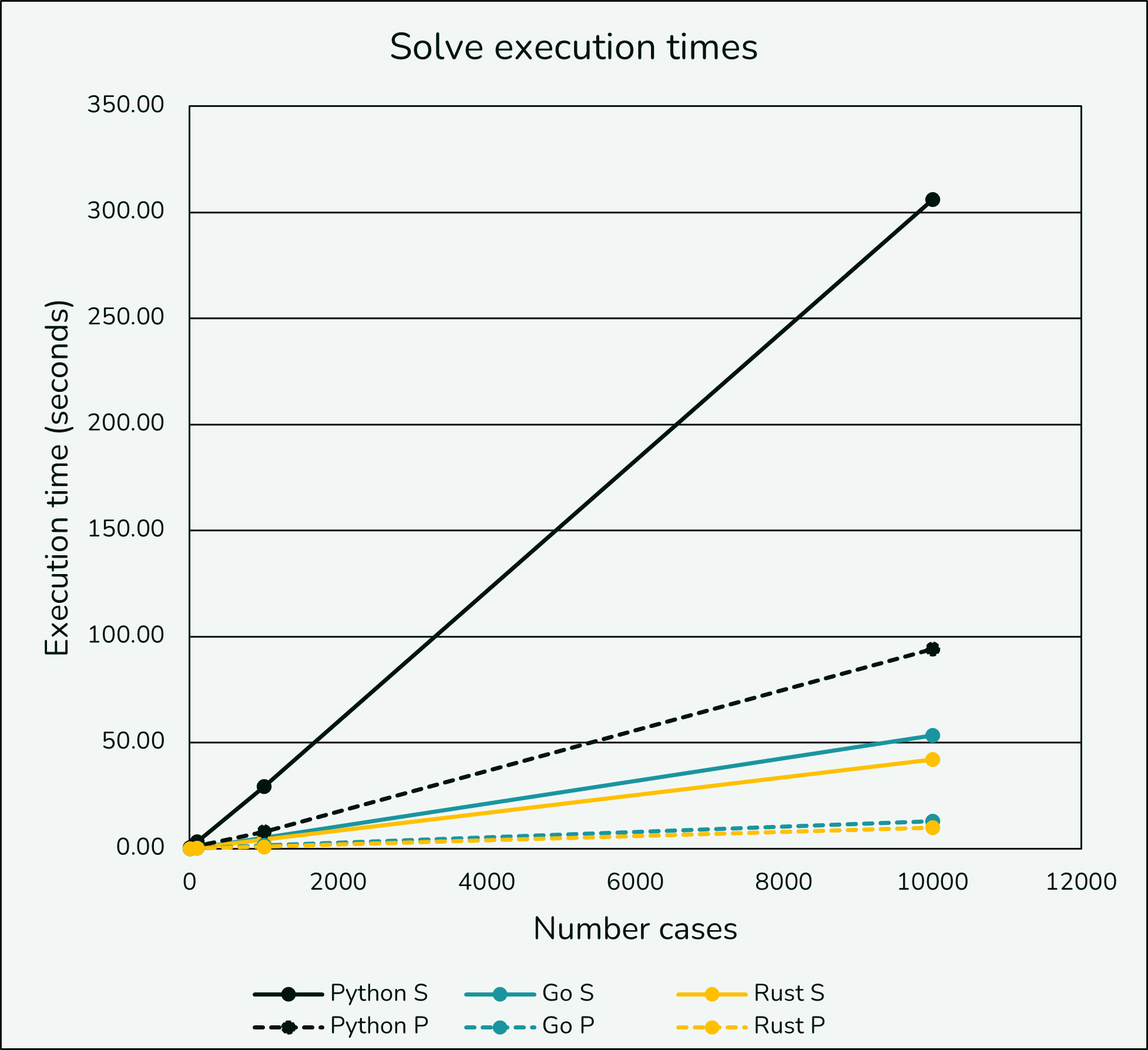
| Implementation | 10 Cases | 100 Cases | 1,000 Cases | 10,000 Cases |
|---|---|---|---|---|
| Python - single | 0.38 | 3.28 | 29.41 | 306.1 |
| Go - single | 0.06 | 0.49 | 5.23 | 53.4 |
| Rust - single | 0.05 | 0.46 | 4.21 | 41.9 |
| Python - parallel | 0.64 | 1.35 | 7.94 | 94.1 |
| Go - parallel | 0.02 | 0.17 | 1.51 | 12.9 |
| Rust - parallel | 0.01 | 0.11 | 0.91 | 10.0 |
Execution time still appears linear, though single threaded Python is noticeably slower than the rest of the implementations.
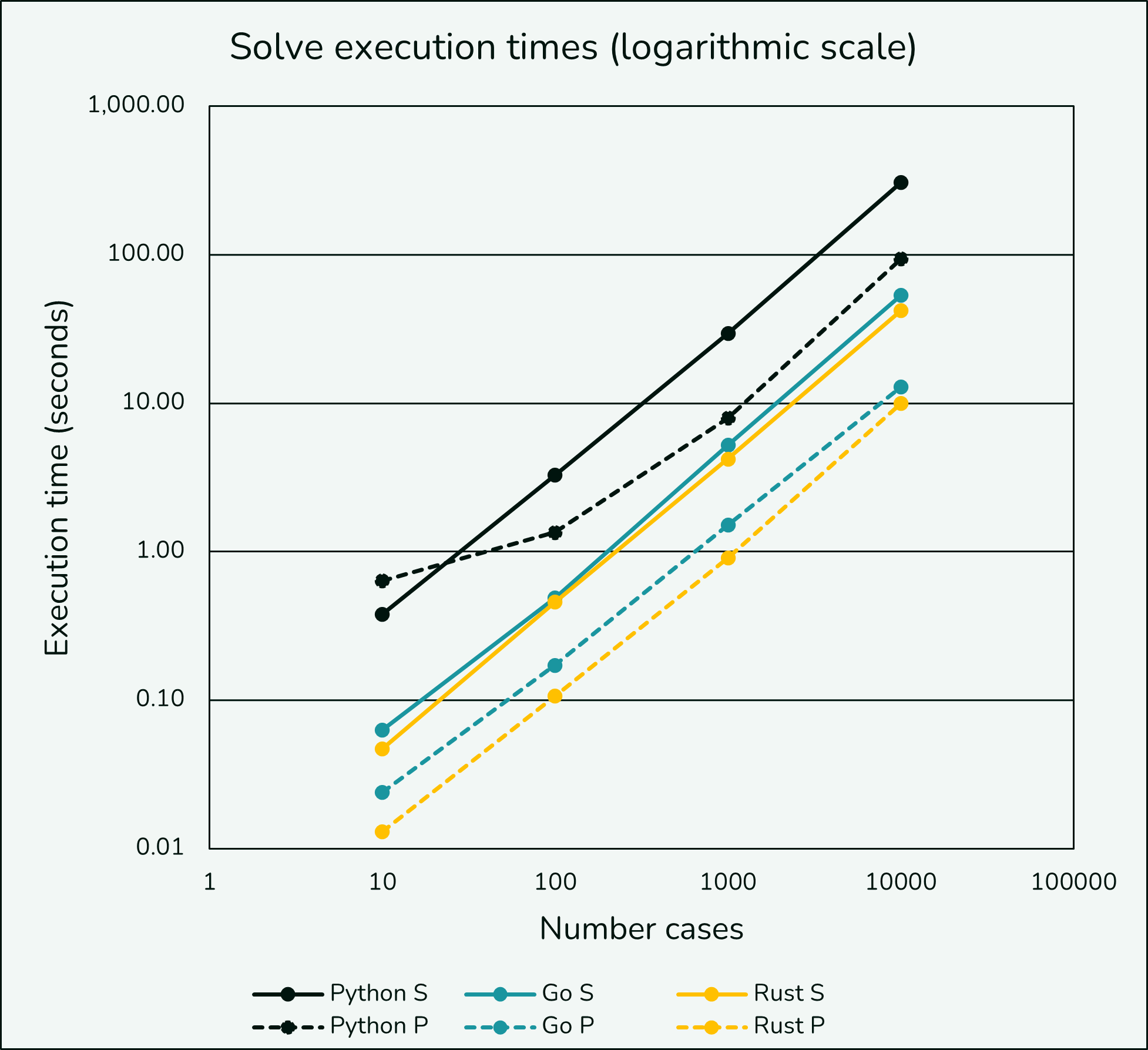
The logarithmic view is helpful and we still see parallel Python getting penalized at low case counts but it overtakes single threaded Python sooner. Note that Go and Rust with single workers appear faster than parallelized Python in this testing and there is nearly a whole order of magnitude difference between parallel Python and parallel Rust.
CONCLUSION
Unsurprisingly, Python, Go, and Rust all performed substantially better than Excel from a run time perspective, especially when parallelizing the workflow. To be clear, I’m not advocating for eliminating Excel even if you can get speed improvements elsewhere. We’ve waived away a lot of real-world complexity that comes with these solutions, and I do not claim the parallelization to be optimal (which may distort the comparisons), but if you were curious about the direction things could take and wanted some information on speed I hope these results fill that need.
Have questions or feedback? Reach out to let us know!